「思ってたよりずっと解きやすかった」
「難しくなってよかった〜」
史上最高難易度を叩き出した2023年の九州大学理系数学。
難化が続いている傾向に怯えながら本番を迎えた受験生も少なくないでしょう。
いざ蓋を開けてみると、思ったよりずっと簡単！
（あ、一般的にみたら難しいので、そこは誤解しないようにしてくださいね笑）
問題を見て気持ちが楽になった受験生も少なくないはず。
この記事では、
『2024年の九州大学・理系数学』を徹底的に分析して傾向やこれからの対策についてお話ししていきます。
これから九大を目指す受験生！
この記事を最後まで読んで、是非とも合格に役立ててください。
この記事で解決できるお悩み
- 九州大学理系数学2024の難易度
- 九州大学理系数学2024の合格ライン
- どんな勉強をしたら九大の数学が解ける？
- これから難しくなるのか？
この記事を書いた人
中原 遼太郎
九大受験に特化した学習塾『竜文会』代表
『竜文会』開校後、初年度には国立大学医学部や九州大学に合格者を輩出。
２年目には旧帝大医学部にも合格！
九州大学の過去問を20年分以上分析して指導カリキュラムを作成。
九州大学医学部に現役合格した経験を生かして、『学習計画の作成』や『LINEでのいつでも相談』による１人１人のサポート・九州大学に特化したハイレベルな演習で「九大受験生」をサポート。
経歴
- ラ・サール高校卒業 （高校入学組中）主席・学校賞受賞
- 九州大学医学部医学科卒業
- 九大本試験 数学・理科 ９割
- 駿台九大実践 ３位
- 九大オープン ６位（数学１位）
※ すべて医学科の成績です - CBT 九大医学部で３位
- ブログ読者 55万人を突破！
もっと知りたい方は中原先生の紹介へ！
※ 当ブログでは、九大受験生や親御様の悩みをリサーチした上で、表面的な悩みだけでなく根本的な悩みを解決できるようなコンテンツ制作を心がけています。コンテンツ制作は、中原遼太郎（九州大学医学部卒・竜文会代表）が担当。制作の流れや想いに関しては、コンテンツ制作ポリシーページを参考にしてください。
九州大学・理系数学2024 全体講評
めっちゃ丸くなったじゃん！
これが私の素直な感想です。
ほとんどの受験生も過去問とのギャップに驚いたはず。
泣いて試験会場を出てくる受験生が多かった2023年に比べて、2024年は試験終わりに笑顔がたくさん見られました。
試験の難易度が適切かどうかはさておき、
数学が『苦手な人』『普通な人』『得意な人』できっちり差が出る入試としてはしっかり機能する試験といえるでしょう。
| 大問 | 難易度 | 目標得点 |
| 第１問 | 簡単 | 50点（医学科） 50点（他学部） |
| 第２問 | やや難 | 30点（医学科） 20点（他学部） |
| 第３問 | やや難 | 30点（医学科） 30点（他学部） |
| 第４問 | 簡単 | 50点（医学科） 50点（他学部） |
| 第５問 | 標準 | 50点（医学科） 30点（他学部） |
| 全体 | 標準 | 210点（医学科） 180点（他学部） |
※難易度は５段階で判断していますが、各段階の詳しいことは後で説明しています。
医学科で210点、他の学部では180点。
2024年の目標点数はかなり高い。
もちろん、これよりも低い点数で合格することは可能です。
余裕を持って合格したいなら取って欲しい点数と思ってください。
ちなみに、2023年の目標点は
医学科で150点、他の学部では100点でした。
目標点はかなり上がっており、特に他学部では100点→180点と大幅な上昇です。
理由としては、
難しい問題が少なかったんですよね。
第２問の（２）とか第３問の（３）は難しいな〜って感じなんですけど、それ以外は典型問題なんですよね。
しっかり数学を勉強していたら解けるでしょ？
ということで、目標点はかなり高めに設定しました。
九州大学・理系数学2024 合格ライン
では、何点取れば合格できるでしょうか。
上でお話ししたのは目標点。
「このくらい取れたらいいなぁ〜」という理想の点数です。
ここでは、最低限とっておいてほしい合格最低ラインの点数をお話しします。
上で書いた目標点は最低ラインではありません。
「このくらいの点数を取れば余裕で合格できるよ」という目安です。
なので、目指すべきなのは先ほどお話しした目標点。
合格最低ライン
-
医学科・・・190点
-
薬学部 臨床薬学科・・・140点
-
理系の他学部・・・130点
数学が苦手な生徒はこの点数を目標にしてください。
ただ、今年は例年よりかなり高めです。
というのも、解きやすい問題と難しい問題がはっきり分かれてたんですよね。
例えば、第１問とか第４問はめちゃくちゃ簡単なんで、数学が苦手でも満点の50点を取って欲しいです。
と考えると、数学が苦手でもこのくらいの点数は欲しいかな〜と思います。
共通テストや２次試験の他の科目が合格者平均点くらい取れるときの最低ラインの点数と考えてください。
もちろん、これらの点数はあくまで目安です。
これより低くても英語や理科でカバーして合格するのは全然余裕なので、あくまで勉強の参考にしてください。
九州大学・理系数学2024
各大問の講評
それでは各大問ごとに「難易度」や「何点取ればいいのか」といったことを話していきます。
各大問ごとに書いてある表の説明をすると、
難易度
難易度は簡単・やや簡単・標準・やや難・難の５段階で評価しています。例年の九大受験生のレベルを参考に判定。標準の問題が合格するには解けないといけないレベル。やや難は解けたら合格者の中でも差がつくレベルと思ってください。
理想解答時間
試験本番でその大問にかける時間です。この時間内で完答できたら合格できる、という時間です。
目標得点
理想時間をかけて解答した時に、合格するために試験本番でとって欲しい点数。受験生はこの点数が取れるかどうかを目安に過去問演習をしましょう。
九大理系数学2024第１問 講評
| 単元 | ベクトル（数B） 微分（数Ⅱ） |
| 難易度 | 簡単 |
| 理想解答時間 | 15分（医学科） 20分（他学部） |
| 目標得点 | 50点（医学科） 50点（他学部） |
※九大数学は各大問 50点満点です。
第１問は満点を余裕で狙える問題。
と言いますか、第１問で満点を取れない場合は確実に不合格。
そう断言していいほど簡単な問題です。
なんでこの問題出した？
こんな問題解けない受験生いないでしょ？
試験問題として機能してんの？
って感じのめちゃくちゃ簡単な問題です。
九州大学を目指して数学を勉強している方なら解けて当たり前の問題。
テーマはベクトル×数Ⅱの微分で、文系数学としても簡単と思える問題でした。
設問分析
（１）ベクトルの基本的な問題。
はっきり言って教科書レベルの問題です。
平行なベクトルは実数倍で書けることを知っていたら簡単に証明できます。
（２）はベクトルと三角形の面積を絡めた問題ですね。
ベクトルの三角形の公式で面積の関数を求めて微分する、といったどんな問題集にも出てくるような典型的な問題。
６乗が出てきて複雑になるかと思いきや、置換するとただの３次関数の最小値を求める問題に帰着できます。
スラスラ解けて当たり前。
50点を無条件でくれるサービス問題でした。
この問題から得られる教訓ですが、
はっきり言ってこのレベルの問題は手が止まらずにスラスラ解けるレベルに到達していないと話になりません。
九大を受けるレベルの生徒ならこんな問題は誰でも解けます。
解けなかったら、不合格の可能性がかなり高いでしょう。
なので、この問題は「解けたら大丈夫！」と安心するのではなく、解くときに戸惑ったらまだまだ数学のレベルが足りないと考えてください。
理想解答時間は設定しましたが、焦って満点を取れないでは意味がありません。
（２）などは計算が上手くいなかい人もいるでしょう。
こういう場合は１題30分と拘らずに、時間をかけてでも正確な答えを求めましょう。
どうせ解けない問題が出てきます。
答えに辿り着ける問題は必要以上に時間をかけても完答するのが合格への秘訣です。
大問が５つで150分だからといって、大問１つを30分で解かないといけないわけではありません。
九大は満点取れなくても余裕で合格できます。
だったら、確実に解ける問題に時間をかけて正確な答えを導いた方が良くないですか？
ちなみにこの大問１は予備校の公表だと標準になっていますが、そんなことはありません。
間違いなく簡単で、50点以外はあり得ない問題です。
九大理系数学2024第２問 講評
| 単元 | 複素数平面（数Ⅲ） |
| 難易度 | やや難 |
| 理想解答時間 | 30分（医学科） 35分（他学部） |
| 目標得点 | 30点（医学科） 20点（他学部） |
n乗根をテーマにした有名な典型問題。
ですが、出題のされ方が珍しかったので難しいと感じた受験生が多かった問題です。
ただ、問われていること自体は難しくありません。
数学が得意な受験生は「あ、こういうことだな！」とパッと分かり、簡単に点数を取ることができたと思います。
設問分析
（１）は出来てほしい！
xのn乗＝１の問題はたくさん解いてきたはず。
移行して因数分解するだけ。
与えられた整式が因数分解の際に出てくる形だと気がつけば何をしたらいいかは簡単に予想がつきます。
（１）の難易度はやや簡単といったところでしょう。
ちょっと聞きたいんですが、
n乗根をテーマにした問題のポイントって整理できてますか？
ここで１つも思いつかない人はヤバいです。
勉強の仕方を少し変えてみましょう。
自分なりにでいいので、『問題のポイント』を言語化してまとめてみる。
これだけでも、切り口が変わった時の対応能力が天と地ほど変わってきます。
（ボックス）
（２）は問題文を見た瞬間にアレルギー反応を起こした受験生が多かったはずです。
「なんか難しそうだから、とりあえず飛ばしておくか」といった感じで、最後まで手をつけなかった人も少なくないでしょう。
ただ、この問題は聞かれることはめちゃくちゃ簡単なんですよね。
単位円を８等分した点（−１と１を除く）をどのように回転させてたら、他のどこかの点に重なるんですか？って聞いてるだけ。
答えは１周もしくは半周。
つまり答えは−１と１です。
あとはこれを言語化して解答するだけ。
複素数平面の問題を普段からグラフに落とし込んで取り組んでいるかどうかで差がついたかもしれません。
問われ方が難しかったので、やや難といったところでしょう。
さて、第２問はかなり点数に差がついたと思います。
特に医学科の受験生は合否を決めた問題になったかもしれません。
おそらく（２）の配点は30点程度ありますから、かなり差がつきます。
一方、他の学部を受けた受験生は（１）を確実に解いておけば「まあ、よし！」といったところ。
（１）が解けるくらいの複素数平面の演習は積むようにしましょう。
九大理系数学2024第３問 講評
| 単元 | 整数（数A） |
| 難易度 | やや難 |
| 理想解答時間 | 30分（医学科） 30分（他学部） |
| 目標得点 | 30点（医学科） 30点（他学部） |
最近の九州大学の整数の難易度を考慮すると解きやすい問題。
それでも、（３）はかなり難易度が高め。
（２）までは解きやすいので確実に解いてほしい問題です。
時間をかけた割に旨みが少ないと言いますか・・・。
設問分析
（１）は明らかに成立する式を証明するだけ。
階乗を数式で表して約分すれば証明終了。
おそらくすべての受験生が解けた問題。
（２）も出来てほしい。
だって、式を見たらどう考えても、a=1、b=2しかあり得なくないですか？
ただ、他の答えがないことを否定しないといけないので（１）を使って解答していきます。
（１）を使うためにaとbの大小関係で場合わけ。
（２）は簡単だからこそ出来るか出来ないかでかなり差がついたはず。
数学では常に前の問題の結果を使うことを意識する。
それを体現したかのような問題。
（３）はやや難といったところでしょうか。
aとbと文字が多いから１文字減らすか〜と考えることができたら勝ち。
不等式を使って文字を減らすことができます。
この１文字減らすっていう発想はめちゃくちゃ使えるので身につけられると強いです。
そして、（１）の形を作るために式を変形していけば答えは自然と出ます。
特に（２）で試されています。
『前問の結果を使う』って当然のことなんですが、自然とできない受験生ってめちゃくちゃ多いです。
次の問題にいった瞬間に、記憶をデリートするんですよね。
前の問題で求めた答えとかどんな解き方をしたかっていうのは次の問題で使えることが多いです。
普段の勉強から意識して取り組んでいきましょう。
九大理系数学2024第４問 講評
| 単元 | 微分法・積分法（数Ⅲ） |
| 難易度 | やや難 |
| 理想解答時間 | 15分（医学科） 20分（他学部） |
| 目標得点 | 50点（医学科） 50点（他学部） |
いい意味でいうと新傾向の問題！
ただ、ずっと考えてもこの問題の出題意図が分からないんですよね。
ただ数え上げるだけだし、しかもそんな複雑でもない。
丁寧に数えた人は、時間をかけずに満点を取ることができた問題でしょう。
第１問と同じで全く差がつかない問題なんですよね。
う〜ん、なんで出題したのか本当に謎。
設問分析
（１）〜（３）まで総じて簡単。
というかめちゃくちゃ簡単な問題！
x軸に水平な直線と垂直な直線。
傾きが正の直線と負の直線。
対称性からこれらの数は等しいはず。
ということで、x軸に水平な直線と傾きが正の直線の本数を求めて２倍するだけ。
x軸に水平な直線の本数なんて見た瞬間わかる。
（それぞれ、３本・４本・５本）
つまり、この問題は傾きが正の直線の本数を正確に数え上げることができますか？って問題。
まじで何を聞いているのか謎。
この問題で言えることはたった１つ。
九大理系数学2024第５問 講評
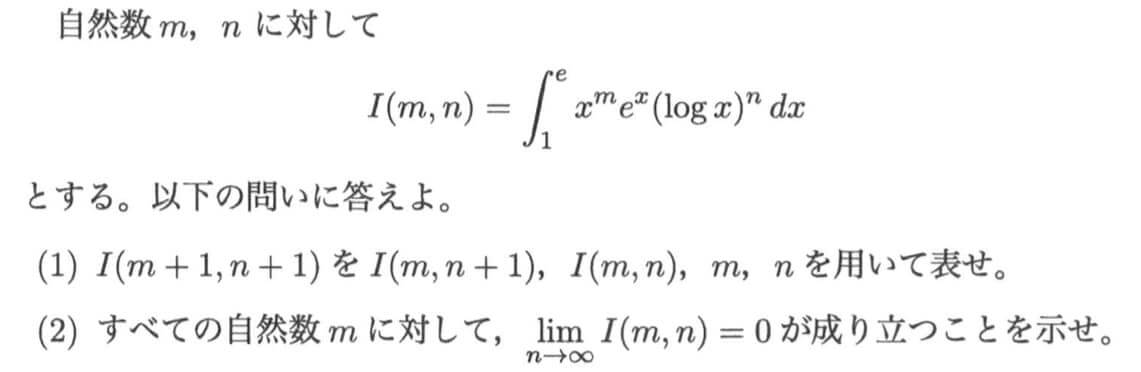
| 単元 | 積分法（数Ⅲ） 極限（数Ⅲ） |
| 難易度 | 標準 |
| 理想解答時間 | 25分（医学科） 30分（他学部） |
| 目標得点 | 50点（医学科） 30点（他学部） |
2024年の理系数学で１番の良問。
数学の勉強の成果が最も発揮された大問でしょう。
この大問で何点取れるか？
医学科以外の学部を受けた受験生にとって合否の分かれ目になった大問です。
（１）は確実に解いてほしい。
九州大学で頻出の積分法（数Ⅲ）の演習をどれだけ積んでいたか？
これが純粋に問われる良問です。
問題は（２）ですね。
難しくないので、ここでどれだけ点数が取れるか。
2024年の受験生の明暗を分けた問題です。
設問分析
（１）積分漸化式。
部分積分をして漸化式を求める典型的な問題。
指数関数＞三角関数＞多項式＞対数関数の順で積分をすると分かっておけばやることは明確なので、簡単に解ける問題。
難易度としてはやや簡単。
問題の（２）！
まず、極限を求めるのにはさみうちの原理を使うどうかを判断できるかがポイント。
ここで聞きたいのですが、
極限の求め方って整理されていますか？
極限を求める解法３つ
・不定形を解消（最高次数で割るとか）
・導関数の定義を利用
・はさみうちの原理を利用
これが整理できておけば簡単なんですよね。
どう考えても、I（m,n）の極限を直接求めることはできないので『はさみうちの原理』確定です。
しかも、（１）で使えそうな式も導出させてますし。
あとは、なとか不等式を引っ張ってくるだけ！
ただ、これはセンスでもなんでもなく、演習量次第です。
九州大学の過去問でも、
積分漸化式に関してはさみうちの原理を原理で極限を求める問題は数多く出題されているので、過去問演習量がものをいった問題でした。
九州大学理系数学の今後の傾向
うちの生徒や九大を目指す受験生に「今年って数学難しくなりますか？」とよく聞かれます。
はっきりいって分かりません。
2022年にはこれ以上難しくなることないと思われた問題が2023年では最高難易度を更新。
すると2024年には一気に難易度が落ちました。
聞かれるたびに答えてますが、考えるだけ時間の無駄です。
要は、難しかろうが簡単だろうが解ける学力をつければいいだけ。
「それができないから聞いてるんでしょ」と怒られそうですが、
どうせやるべき勉強って変わらなくないですか？
入試本番のその日まで１問でも多くこなす！
これを超える対策はありません。
難しくなるかどうか考えるのはただの不毛な時間です。
各予備校がね、「この傾向が続くだろう」とかそれっぽいことを発表してますけど気にしなくていいと思います。
九州大学理系数学の対策法
基本から丁寧に勉強していく。
これにつきます。
いきなり難しい問題を解くのではなく、まずはチャートやFocus Goldで基本的な知識を身につける。
そして、難しい問題集に取り組んでいきましょう。
大事なことは線引きをしないこと。
「このくらい勉強すれば九大は大丈夫でしょ！」という気持ちで勉強すると、難化したときに全く対応できません。
詳しい九州大学・理系数学の勉強法に関しては以下の記事でお話ししています。
是非とも勉強の参考にしてください！
九州大学・理系数学2024 講評 まとめ
今回は九州大学 理系数学2024の講評をしました。
最後に簡単にまとめておきます。
| 大問 | 難易度 | 目標得点 |
| 第１問 | 簡単 | 50点（医学科） 50点（他学部） |
| 第２問 | やや難 | 30点（医学科） 20点（他学部） |
| 第３問 | やや難 | 30点（医学科） 30点（他学部） |
| 第４問 | 簡単 | 50点（医学科） 50点（他学部） |
| 第５問 | 標準 | 50点（医学科） 30点（他学部） |
| 全体 | 標準 | 210点（医学科） 180点（他学部） |
過去問の傾向を分析するのは確かに大事です。
ただ、「このくらい勉強したら過去問は解けそう！」と勝手に線引きするのはやめましょう。
何度も言いますが、難化したときに対応できません。
さらに、あなたの成長の妨げにもなります。
「もしかしたらめっちゃ難化するかも！」と最悪の想定をして、試験当日まで実力を伸ばしてくささい。
