「今年の九大の数学やばかった・・・」
受験生がみんな同じことを言いながら試験会場を出てくる。
中には涙を流しながら出てくる人もいました。
2022年の九州大学理系数学が歴代最高難易度であることは間違いありません。
この記事では、九州大学理系数学2022の徹底解説をしていきます。
受験生が気になる、「難易度」や「何点とったら合格できるのか」と言った情報まで！
すべてを解説していきます。
この記事でわかること
- 九州大学理系数学2022の難易度
- 九州大学理系数学2022の合格ライン
- 各大問ごとの難易度や理想得点
この記事を書いた人
中原 遼太郎
九大受験に特化した学習塾『竜文会』代表
『竜文会』開校後、初年度には国立大学医学部や九州大学に合格者を輩出。
２年目には旧帝大医学部にも合格！
九州大学の過去問を20年分以上分析して指導カリキュラムを作成。
九州大学医学部に現役合格した経験を生かして、『学習計画の作成』や『LINEでのいつでも相談』による１人１人のサポート・九州大学に特化したハイレベルな演習で「九大受験生」をサポート。
経歴
- ラ・サール高校卒業 （高校入学組中）主席・学校賞受賞
- 九州大学医学部医学科卒業
- 九大本試験 数学・理科 ９割
- 駿台九大実践 ３位
- 九大オープン ６位（数学１位）
※ すべて医学科の成績です - CBT 九大医学部で３位
- ブログ読者 55万人を突破！
もっと知りたい方は中原先生の紹介へ！
※ 当ブログでは、九大受験生や親御様の悩みをリサーチした上で、表面的な悩みだけでなく根本的な悩みを解決できるようなコンテンツ制作を心がけています。コンテンツ制作は、中原遼太郎（九州大学医学部卒・竜文会代表）が担当。制作の流れや想いに関しては、コンテンツ制作ポリシーページを参考にしてください。
ぜひ、これからの勉強に役立ててください。
九州大学・理系数学2022 全体講評
「2022年の入試を受けた受験生はかわいそう」
心からそう思える問題セットでした。
過去25年では確実に最高難易度！
京都大学よりもはるかに難しい！
そんな試験でした。
2022年九大数学は過去25年で最高難易度！
| 大問 | 難易度 | 目標得点 |
| 第１問 | 標準 | 50点（医学科） 50点（他学部） |
| 第２問 | やや難 | 25点（医学科） 10点（他学部） |
| 第３問 | やや難〜難 | 25点（医学科） 10点（他学部） |
| 第４問 | やや難 | 50点（医学科） 35点（他学部） |
| 第５問 | やや難 | 30点（医学科） 20点（他学部） |
| 全体 | 昨年より難化 （過去最高難易度） |
170点（医学科） 115点（他学部） |
・難易度は５段階で判断していますが、各段階の詳しいことは後で説明しています。
「全体での合計点が各大問と合ってなくない？」
と思われたかもしれません。
それぞれも大問が重たく時間がかかる問題なので、150分では全部を解くのが難しい。
だから、合計点での目標点は少し低めに設定しています。
例年の目標点は、
医学科が200点、他学部が150点程度ですが、
約40点下がっています。
（しかも、さらに低くても合格することはできます！）
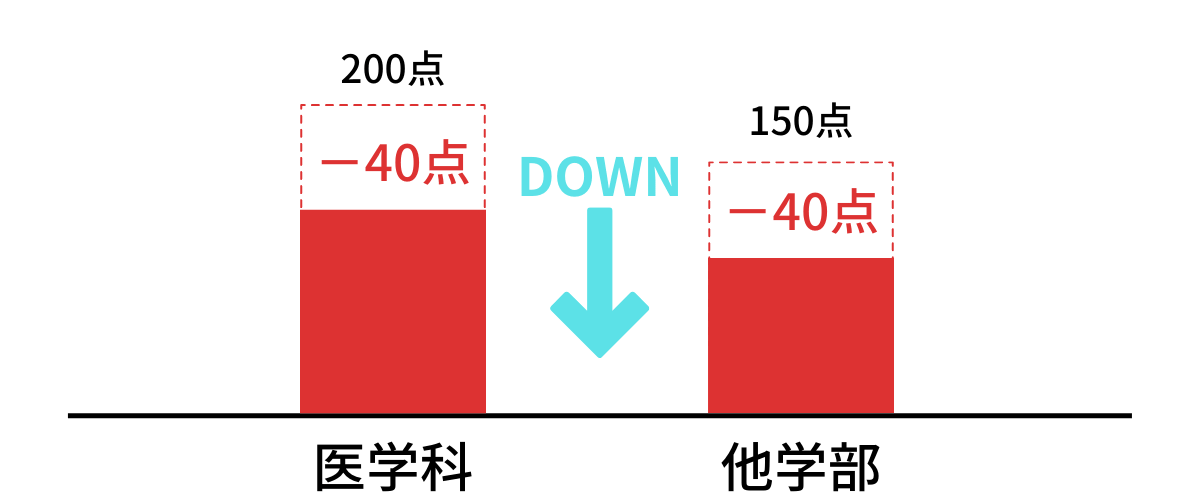例年より目標点数は40点も下がる結果に
受験生の感想を見ても、「難しくてやばかった」という声が多く、多くの受験生を苦しめた試験になりました。
九州大学・理系数学2022 合格ライン
では、何点とれば合格できるのでしょうか？
合格最低点をもとに、合格最低ラインを考えていきます。
上で書いた目標点は最低ラインではありません。
「このくらいの点数が目指す目安」というもの。
これから過去問を解く際の参考にしてください。
合格最低ライン
-
医学科・・・140点
-
薬学部 臨床薬学科・・・95点
-
理系の他学部・・・70点
合格最低点や共通テストのボーダー、英語や理科の２次試験の難易度を元に作成しています。
（英語は例年の得点傾向から、採点基準を分析し合格平均点を予想しております。）
共通テストや２次試験の他の科目が合格者平均点くらい取れるときの最低ラインの点数と考えてください。
あくまで目安であり、この得点より低くても合格している人はもちろんいます。
参考程度にしてください。
九州大学・理系数学2022
各大問の講評
それでは各大問ごとに「難易度」や「何点取ればいいのか」といったことを話していきます。
各大問ごとに書いてある表の説明をすると、
難易度
難易度は簡単・やや簡単・標準・やや難・難の５段階で評価しています。例年の九大受験生のレベルを参考に判定。標準の問題が合格するには解けないといけないレベル。やや難は解けたら合格者の中でも差がつくレベルと思ってください。
理想解答時間
試験本番でその大問にかける時間です。この時間内で完答できたら合格できる、という時間です。
目標得点
理想時間をかけて解答した時に、合格するために試験本番でとって欲しい点数。受験生はこの点数が取れるかどうかを目安に過去問演習をしましょう。
九大理系数学2022第１問 講評
第１問は九州大学理系数学2022で１番解きやすい問題です。
この大問で満点を取らなければ合格はありえません。
| 単元 | 空間ベクトル（数B） 図形と方程式（数Ⅱ） |
| 難易度 | 標準 |
| 理想解答時間 | 15分（医学科） 20分（他学部） |
| 目標得点 | 50点（医学科） 50点（他学部） |
※九大数学は各大問 50点満点です。
難易度は標準ですが決して簡単な問題ではありません。
「数学が得意でも苦手でもなくて、普通〜」みたいな人には少し難しい。
そんな難易度になります。
設問分析
問題は空間ベクトルの標準的な問題です。
２つのベクトルに垂直な単位ベクトルを求めて、平面との対称点を求め最短距離を求める。
１つ１つの解法は、ザ・典型問題！
あとは、どれだけ反射的に解けるか、で全てが決まります。
（１）垂直なベクトルを文字でおき、内積が０を使えば終了
（２）（１）で求めた単位ベクトルを利用してPP’と平面との交点を実数を用いて表す。あとは内積を用いたら終了です。
図形と方程式の単元で頻出の「直線に対する対称点の求め方」の問題です。
- 中点を利用する方法
- ベクトルを利用する方法
の２つがありますが、両方で解けるようになっておきましょう。
私は毎年、生徒に２つの解法を説明しています。
どちらかだけではなく、基本的な解法を全部マスターしておくことが重要です。
（３）（２）ができたら簡単です。
（点PとQが平面に対して同じ側にあることを言わないといけないですが、、、）
「P‘とRとQが一直線上にある時が最短距離」という頻出の知識で解けます。
この問題は50点を取らなければなりません。
九大数学は３問完答すれば大丈夫！
30~40分かけてもいいので、正確に答えを導きましょう。
第１問は時間をかけてでも完答必須！
理想解答時間は15〜20分と書きましたが、本番では30〜40分かけてもいいのでこの問題は完答しましょう。
分からない問題は捨てて、2〜3問解ければいいので、時間をじっくりかけてでも簡単〜標準的な問題は満点を取ることが大事！
時間をかけてでも正確な値を出せた人が合格できました！
九大理系数学2022第２問 講評
| 単元 | 式と証明（数Ⅱ） 極限（数Ⅲ） |
| 難易度 | やや難 |
| 理想解答時間 | 30分（医学科） 35分（他学部） |
| 目標得点 | 30点（医学科） 20点（他学部） |
しっかり勉強していればそこまで難しくない問題。
でも（１）が見慣れない問題であることと、式と証明の単元が苦手・対策不足の受験生が多いこと、（３）の極限が数Ⅲの計算練習をかなり積んでおかないと難しいことから「やや難」としました。
設問分析
（１）は数学に慣れていないと難しい。
どのように証明したらいいか分からなかった受験生が多かったと思われます。
しかし、式と証明の「整式の割り算」の解法をいくつか覚えておけば簡単に解くことができます。
解法自体は難しくなく、あとは試験本番で「この時はこう解く！」という知識をしっかり発揮できるかにかかっています！
（２）は簡単、商を消すようにαとβを代入するだけ。
求める式に対して条件式が足りないので、与えられた式を微分して条件式を増やしましょう。
（２）は「簡単な」問題！（２）だけでも解けなくてはなりません。
（３）は極限の計算練習を積んでいた人にとったら簡単です。
（しかし、相当の練習を積まないといけないのでほとんどの受験生にとっては難しかったと思います。）
不定形が解消できないタイプの極限の問題に対して、「導関数の定義」から導く。
という解法を持っていたら簡単に解けます。
どんな問題でも、（２）だけ、（３）だけ、でも解ける問題がないか探しましょう。
物理などでも、「最後の問題だけは解けた」なんてことはよくあります。
必ずすべての範囲を漏れなく勉強しましょう。
「式と証明の単元は頻出ではないから」、と数Ⅲに時間を回してしまう人がいます。
もちろん頻出単元を重点的に勉強するのは大事！
しかし、もしもの時のために、すべての範囲をしっかり勉強しておきましょう！
※クリックしてもLINEが自動で開かない場合は、
『LINEアプリを開く』を押してください。
九大理系数学2022第3問 講評
| 単元 | 整数（数A） |
| 難易度 | やや難〜難 |
| 理想解答時間 | 35分（医学科） 40分（他学部） |
| 目標得点 | 25点（医学科） 10点（他学部） |
2022年の九州大学理系数学で１番の難問。
整数問題を解き慣れていない人からしたら、絶望しか感じません。
理想解答時間は書きましたが、本番では解けなくていい問題です。
欲を言えば、（２）まで解いて30点を確保する問題です。
設問分析
（１）は互いに素を背理法で証明する問題。
「互いに素を仮定して、差をとって矛盾を導く」という一連の流れを何回も練習していれば簡単です。
ただ注意しないといけないのが、整数であることも示すこと！
今回は「互いに素」かつ「整数」を証明しないといけません。
整数の解法３つ
・（素）因数分解をする
・不等式で評価する
・余りに着目する
が頭に入っていればそんなに難しくありません。
「平方数の余りの特徴」に関する問題なので、解法は体系的に考えることで思いつきます。
それでもやはり経験不足だと難しい！
整数は重要単元なので、しっかり演習を積んでおきましょう。
（３）は「存在証明」の問題。
「条件を満たすものを１つ求めよ」という、途中式は必要なく条件を満たすものを１つ、無理矢理でもいいので求めたら満点！
という問題です。
ただ（１）と（２）を使って工夫しないといけないのと、「存在証明」の問題をたくさん解いたことがある人は少ないので難問に分類しました。
本番では解けなくて大丈夫です！
慣れてくると点数も安定してくるので、差を一気につけることができます！
たくさん練習を積みましょう！
九大理系数学2022第4問 講評
| 単元 | 微分法・積分法（数Ⅲ） |
| 難易度 | やや難 |
| 理想解答時間 | 25分（医学科） 30分（他学部） |
| 目標得点 | 50点（医学科） 35点（他学部） |
超新傾向の問題！
受験生は見た瞬間、「共通テスト？？」と思ったはず。
テーマとしては、「区分求積法」の導出。
難易度自体は難しくなく、数Ⅲで面積評価の取り扱い方に慣れていれば簡単。
ただ、試験本番で新傾向に戸惑うことも考慮して「やや難」の設定としました。
設問分析
（１）は「導関数の定義から導関数を求める」ことを普段から練習している人は簡単。
確実に得点しておきたい問題。
（２）は平均値の定理を用いてと書かれており、ただ公式を用いるだけ。確実に解答！
（３）から少し難しい。
とは言っても、「1/n幅で面積評価」することを問題文に与えられた定積分の性質を用いてさせているだけ。
②式の形から、「あ、面積評価だな」と思ったら勝ち！
積分の演習量がものを言う良問でした。
（４）は工夫して1~nまでの和を取るだけ。
「面積評価の問題」を解法は全く同じ。
右の不等式を解くときに、やや工夫が必要だが、最終的な形はすでに与えられています。
ただゴールを目指して式変形をしていだけ！
第１問の完答は当たり前として、第４問は合否を決めた問題と思います。
今年は合格最低点がかなり低く、人によっては数学は100点でも余裕で合格した人がいたはず！
と言うことはこの問題が超重要！
第４問が合否の分かれ道！
九大理系数学2022第５問 講評
| 単元 | 積分法（数Ⅲ） |
| 難易度 | やや難 |
| 理想解答時間 | 35分（医学科） 45分（他学部） |
| 目標得点 | 30点（医学科） 20点（他学部） |
第５問にしてこの計算をさせるか・・・
というほど、計算量がやばい。
5tを見た瞬間絶望した受験生もいたのではないでしょうか？
第５問は計算量の多さに絶望...
特に工夫をせずに計算した受験生は解答用紙が足りなくなったはず。
そもそも第５問にこの問題を出して、受験生は集中力が残っていたのか疑問です笑
計算がやばい・・・
ことを除くと標準〜やや難の問題。
媒介変数で表された関数のx軸対称を示すときに困ったくらいでしょう。
設問分析
（１）は計算するだけ。簡単な問題。
ただ普段から「和積の公式」の導出の練習を行い、ある程度は頭の中でできるようになっておきましょう。
本問では和積や積和の公式を使う箇所が多く、いちいち導出していては試験時間内に終わるのが厳しくなってきます。
時間との勝負の問題に威力を発揮します。
（２）も簡単。
媒介変数で表されたグラフを書く練習、面積を求める練習をしっかり積んでおけば余裕で解けます。
ここまでは絶対に解けてほしい問題。
（３）の前半はx軸対称の定義を知っているどうかのやや知識問題。
後半は示すことは簡単ですが、計算が工夫しないとやばいです。
「回転→複素数」という発想で複素数平面に持ち込んだ後に、π/3を代入して加法定理で展開してしまったら解答用紙が真っ黒。
日々の練習から「どうやったら工夫できるか」の視点を持って問題を解きましょう。
（４）は（２）の図示さえ出来ていたら簡単です。
（３）はまったく分からなくても簡単に解けます。
第２問と同じで、前半が分からなくても後半は解ける問題。
こういう問題を絶対に落とさないようにしよう。
いきなり本番で実践するのは難しいです。
いつもの勉強も本番のように取り組む！
これが本番で結果を残すための秘訣です。
問１.2ができなくて問３を諦めるなんて絶対NG
九州大学・理系数学2022
九州大学受験生によるレポート
では実際に九州大学の2022年の入試を受験した生徒にレポートを書いてもらいました！
２次試験本番に「どのように感じたのか、どの順番で問題を解き進めたか」を赤裸々に語ってもらいました！
第１問
全員取れるなと思いました。基本的な問題で満点を取らないといけないなと思い、「とにかくミスしないように」と注意しながら解いて、20分くらいで完答。
第２問
ちょっとよく分からないなと思いました。
「ん、存在することを示せ」ってどういうこと？
と思ったけど（２）は解けそうだなと思いました。
（２）を解いて、（３）は計算が面倒くさいなと思って保留。
第３問
（１）は「互いに素を証明する」簡単な問題ですぐにとけた。
（２）は変形したらいけそうかな〜と思い、10分くらい数式をいじってみたがうまくいかなかった。とりあえず（２）を利用して（３）を求めようとして、検索してみたが答えは出なかった。
（「１つ答えを見つけよ」だから、いろいろ代入したが無理でしたね笑）
第４問
長くて読みたくないなと思い、飛ばして第５問にいきました。
（10秒で速攻スキップ！）
第５問
基礎的な問題に見えるが、本当に簡単のなのだろうかと思い解答開始。
（１）と（２）は難しくなかったので、「落とさないように」と気をつけながら計算
（３）は前半は解いたが、後半は回転だから虚数をかけたらなんとかなるかと思ったが撃沈。
（４）は（３）が解けないと無理だなと思い、一旦解答終了。
第４問に戻って
（１）の前半は教科書通りの定義の問題で簡単。後半はどのように定義域を用いたらいいか悩んで、誤魔化して解答。
（２）平均値の定理と分かったが一旦飛ばす。
（３）を見ると、面積評価ぽかったので、挟んでシンプルに解答。
（４）はSnの式の和をとったらいけると思い、条件式を用いて解答。
あとはぼーっとしたり、整数問題に取り組んでいたら試験時間が終了！
※クリックしてもLINEが自動で開かない場合は、
『LINEアプリを開く』を押してください。
九州大学理系数学の今後の傾向
2021年も難化しましたが、2022年はさらに難化しました。
「難しくなったら次の年は簡単」という暗黙の了解を無視するような難易度。
九大受験生はこの難易度が続くと思って勉強した方がいいと思います。
2000年代〜2010年代は解きやすい、いわゆる「標準的な」問題の出題が多かったです。
しかし、近年は「標準的な」問題は少なく、旧帝国大学らしい「やや難」の問題が多くなってきています。
（新傾向の問題も多く、思考力を普段から培う練習が必要不可欠！）
私は今後、高い難易度で九大数学の試験レベルは落ち着くと思います。
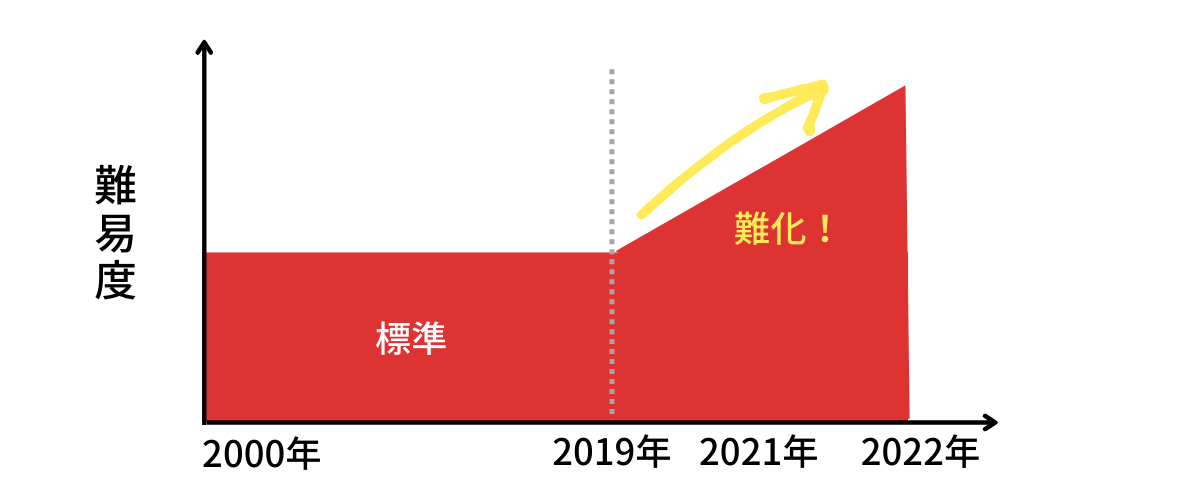九大数学の問題は年々難化。今後もレベルが落ちることはない！？
九州大学理系数学の対策法
過去問をたくさん解くことの対策は意味がないです。
というのも2000年代の過去問を見ると、まったく別物になってきています。
校１年生から「チャート式」や「Focus Gold」で基礎力を鍛え、高校２年生からは少しずつ「大学への数学 １対１対応の演習」といった難しい問題集に取り組んでいきましょう。
高校の授業で扱う問題だけでは、絶対に解けるようにはなりません。
少なくとも、九大の理系数学で勝負するレベルにいくのは不可能です。
※クリックしてもLINEが自動で開かない場合は、
『LINEアプリを開く』を押してください。
九州大学・理系数学2022 講評 まとめ
今回は九州大学 理系数学2022の講評をしました。
数学が少しできる程度では、できない人と同じ点数になってしまう
そんな問題でした。
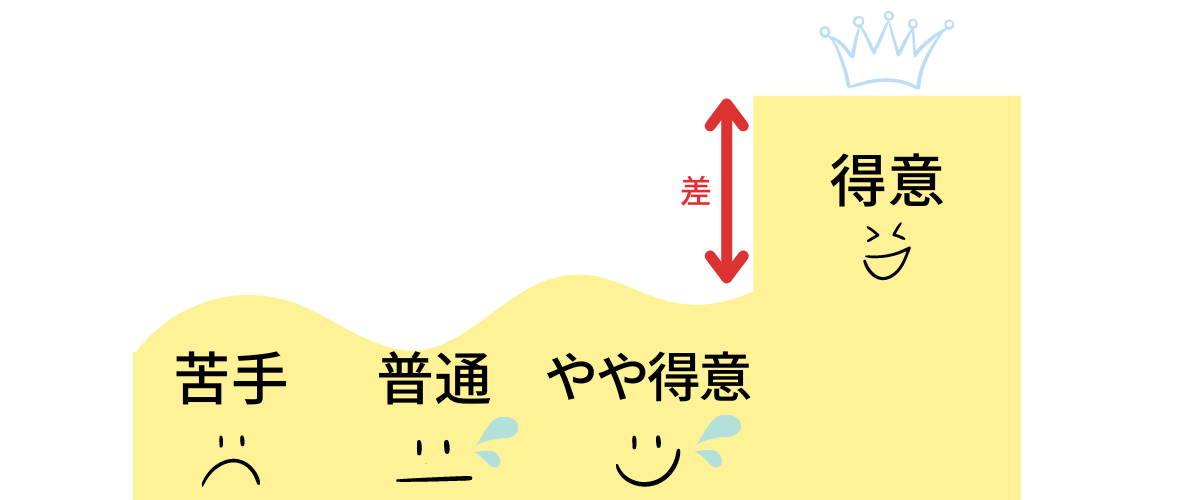数学が苦手〜やや得意な人は差がつかないような結果に...
表を最後にもう１度書いておきます。
| 大問 | 難易度 | 目標得点 |
| 第１問 | 標準 | 50点（医学科） 50点（他学部） |
| 第２問 | やや難 | 25点（医学科） 10点（他学部） |
| 第３問 | やや難〜難 | 25点（医学科） 10点（他学部） |
| 第４問 | やや難 | 50点（医学科） 35点（他学部） |
| 第５問 | やや難 | 30点（医学科） 20点（他学部） |
| 全体 | 昨年より難化 （過去最高難易度） |
170点（医学科） 115点（他学部） |
数学は勉強に終わりがありませんし、満足する点数を取ろうと思ったら膨大な時間が必要になります。
今すぐにでも勉強を始めましょう。
それだけで、あなたの九大合格の可能性は何倍にも上がります。
こちらもCHECK
-
-
九州大学に合格する勉強法・対策まとめ〜信じられないほど成績UP〜
「九大に受かるための勉強法が知りたい！」 この記事では、あなたのこんな質問に徹底的に答えていきます。 「九州大学に絶対合格したい」 という気持ちに応えるべく、 『九州大学合 ...
続きを見る
